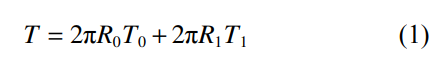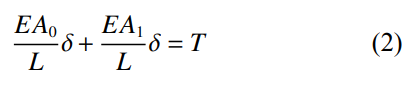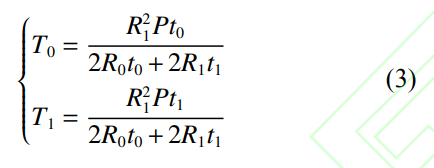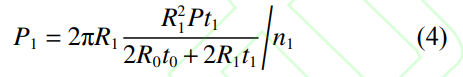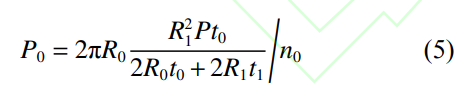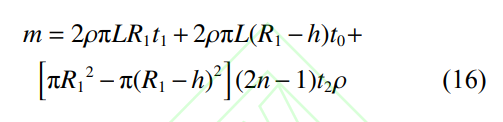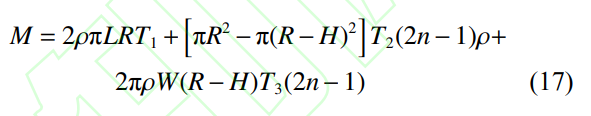引言

輕質(zhì)高承載是船舶與海洋工程領域結(jié)構(gòu)設計的重要需求，加筋圓柱殼作為一種優(yōu)良的承載結(jié)構(gòu)，具有受力均勻、強度和承載能力高、制造與裝配簡單等優(yōu)點，已被廣泛應用于水下航行器結(jié)構(gòu)設計。當雙層圓柱殼和單層圓柱殼的厚度相同時，雙層圓柱殼結(jié)構(gòu)形式能夠滿足強度和承載能力的要求，且臨界壓力還有較大的優(yōu)勢，承載效率更高，同時雙層圓柱殼結(jié)構(gòu)要求的板厚更薄，具有更好的制造可行性[1]。胡子嘯等[2]利用有限元方法計算分析了等質(zhì)量不同結(jié)構(gòu)形式鋼質(zhì)雙層加筋圓柱殼的強度和承載能力，結(jié)果顯示相較于單層加筋圓柱殼結(jié)構(gòu)，同等重量的I形加強筋雙層圓柱殼的極限承載能力明顯更高。針對雙層加筋圓柱殼的強度計算問題，夏賢坤等[3]直接利用耐壓液艙強度計算方法進行了應力和穩(wěn)定性分析，然而由于其受力形式與附著于單層殼體局部外表面的耐壓液艙存在一定的差異，導致計算結(jié)果與實際情況存在較大偏差；曹曉明等[4]提出了內(nèi)、外殼體縱向力的計算模型，建立了雙層圓柱殼結(jié)構(gòu)在外壓載荷作用下應力的解析計算方法，結(jié)果顯示計算結(jié)果與有限元結(jié)果吻合較好。

夏賢坤等[5]針對鋼質(zhì)雙層圓柱殼結(jié)構(gòu)，基于解析法的強度和穩(wěn)定性約束條件進行優(yōu)化設計，分析了該種結(jié)構(gòu)形式與鋼質(zhì)單層耐壓殼體結(jié)構(gòu)形式相比所存在的利弊。Ding[6]利用力的平衡條件和環(huán)肋與內(nèi)外殼正交連接的變形協(xié)調(diào)條件，研究了外壓下鋼質(zhì)雙層加筋圓柱殼內(nèi)外殼之間的關系，建立了在均勻靜水外壓作用下縱向和橫向加筋雙層圓柱殼的平衡方程，給出了一種高精度的屈曲理論臨界壓力求解方法。Xue等[7]提出了靜水壓力作用下鋼質(zhì)夾層圓筒管的一階剪切變形理論，推導了夾層圓柱殼的平衡微分方程，獲得了不同長徑比下夾層圓柱殼的屈曲壓力。上述針對雙層加筋圓柱殼結(jié)構(gòu)的研究主要關注的是鋼質(zhì)材料耐壓結(jié)構(gòu)。

鈦合金因具有比強度高、無磁性、耐腐蝕等優(yōu)點被廣泛應用于航空航天、化工能源等領域，近年被應用于船舶領域的深海耐壓結(jié)構(gòu)。江翔[8]以新型鈦合金單層加筋圓柱殼結(jié)構(gòu)為研究對象，進一步對圓柱殼臨界壓力公式進行了修正，通過有限元軟件對圓柱殼的強度和穩(wěn)定性進行了分析計算，并結(jié)合相關規(guī)范對其強度進行了校核，隨后在特征屈曲的基礎上進行了非線性分析。李艷萍[9]通過有限元軟件ANSYS建立了鈦合金圓柱殼有限元模型，分別進行了強度、穩(wěn)定性及疲勞分析，并基于BP神經(jīng)網(wǎng)絡代理模型，采用遺傳算法對結(jié)構(gòu)進行了優(yōu)化設計。Ge等[10]采用有限元軟件建立了鈦合金環(huán)肋加筋圓柱殼結(jié)構(gòu)有限元模型，并對角焊產(chǎn)生的殘余應力和變形進行了數(shù)值模擬，分析了其對整體結(jié)構(gòu)承載能力的影響。劉楨[11]通過數(shù)值模擬對鈦合金單層圓柱殼的碰撞凹陷進行了分析，利用ANSYS屈曲分析模塊分析了球冠狀凹陷半徑、凹陷深度以及凹陷位置對圓柱殼屈曲臨界載荷的影響，并與完整無凹陷的鈦合金單層圓柱殼計算結(jié)果進行了對比分析。Zhang等[12]為準確模擬鈦合金環(huán)肋圓柱殼在深海環(huán)境下的失效模式，對環(huán)肋圓柱殼的極限強度進行了分析，并對環(huán)肋圓柱殼在不同屈曲模式下的應力狀態(tài)進行了分析。但上述研究主要聚焦于鈦合金單層加筋圓柱殼結(jié)構(gòu)，針對鈦合金雙層加筋圓柱殼結(jié)構(gòu)的研究很少，在滿足設計要求的情況下，鈦合金雙層加筋圓柱殼結(jié)構(gòu)的極限承載能力和重量相比鈦合金單層加筋圓柱殼結(jié)構(gòu)是否具有優(yōu)勢還有待研究。

另一方面，目前對加筋圓柱殼結(jié)構(gòu)的研究大多只考慮了單一設計要求，如不同長徑比或是不同的計算壓力，而同時全面分析不同設計要求下雙層加筋圓柱殼結(jié)構(gòu)優(yōu)化設計方案特性的研究很少。曹曉明等[13]以鋼質(zhì)雙層加筋圓柱殼強度及穩(wěn)定性要求為約束，以結(jié)構(gòu)重量最輕為目標，建立了優(yōu)化設計的數(shù)學模型，其利用粒子群優(yōu)化算法進行優(yōu)化設計，探究了結(jié)構(gòu)重量隨極限潛深增大的變化規(guī)律。汪靜等[14]以1000m水深的某鈦合金海底觀測儀單層耐壓殼體為研究對象，通過線性屈曲和非線性后屈曲分析，得到了不同長徑比模型臨界載荷、極限強度以及后屈曲行為的變化規(guī)律。對于鈦合金耐壓夾層圓柱殼結(jié)構(gòu)，張浩宇等[15]針對特定水深和長徑比圓柱殼，建立了其芯層結(jié)構(gòu)形式的兩階段拓撲優(yōu)化數(shù)學模型，并基于遺傳算法對結(jié)構(gòu)沿著徑向和軸向進行了芯層布置形式的拓撲優(yōu)化。

為全面、客觀評估鈦合金雙層加筋圓柱殼結(jié)構(gòu)的性能以及相比單層加筋圓柱殼的優(yōu)勢，本文擬以鈦合金雙層加筋圓柱殼結(jié)構(gòu)重量最輕為目標函數(shù)，考慮強度、穩(wěn)定性和尺寸搭配約束條件，建立鈦合金雙層加筋圓柱殼結(jié)構(gòu)優(yōu)化設計數(shù)學模型，然后采用遺傳算法進行求解，分析不同計算壓力和長徑比下優(yōu)化方案的特征應力、約束裕度、極限承載能力以及重量，獲得不同設計要求下鈦合金雙層加筋圓柱殼優(yōu)化設計方案的特性，并與典型單層加筋圓柱殼優(yōu)化設計方案進行對比。

1、有限元模型

1.1幾何模型

本文以鈦合金雙層加筋圓柱殼為研究對象，加強筋拓撲形式選用同等重量下極限承載能力更高的I型加強筋[2]，幾何模型如圖1所示。雙層加筋圓柱殼結(jié)構(gòu)由直徑D=2R1（外殼）、長度L、內(nèi)殼厚度t0、外殼厚度t1、肋骨腹板高度h、腹板厚度t2和肋骨間距s這7個參數(shù)表示。本文設置了單層加筋圓柱殼用于與雙層加筋圓柱殼進行對比分析。單層殼加強筋的形式為T型材，由直徑、長度、殼板厚度、肋骨腹板高度、腹板厚度、肋骨面板寬度、面板厚度和肋骨間距這8個參數(shù)表示。

1.2材料參數(shù)

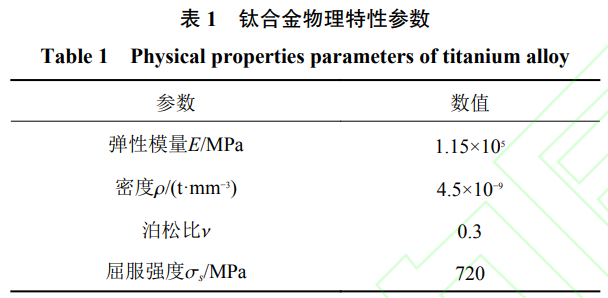
選用鈦合金作為雙層加筋圓柱殼的制作材料，鈦合金的物理特性參數(shù)如表1所示。

1.3單元與網(wǎng)格劃分

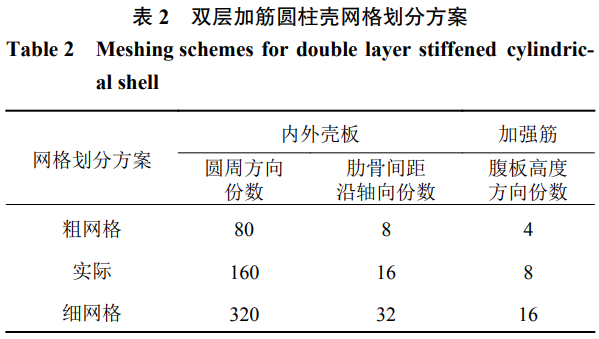
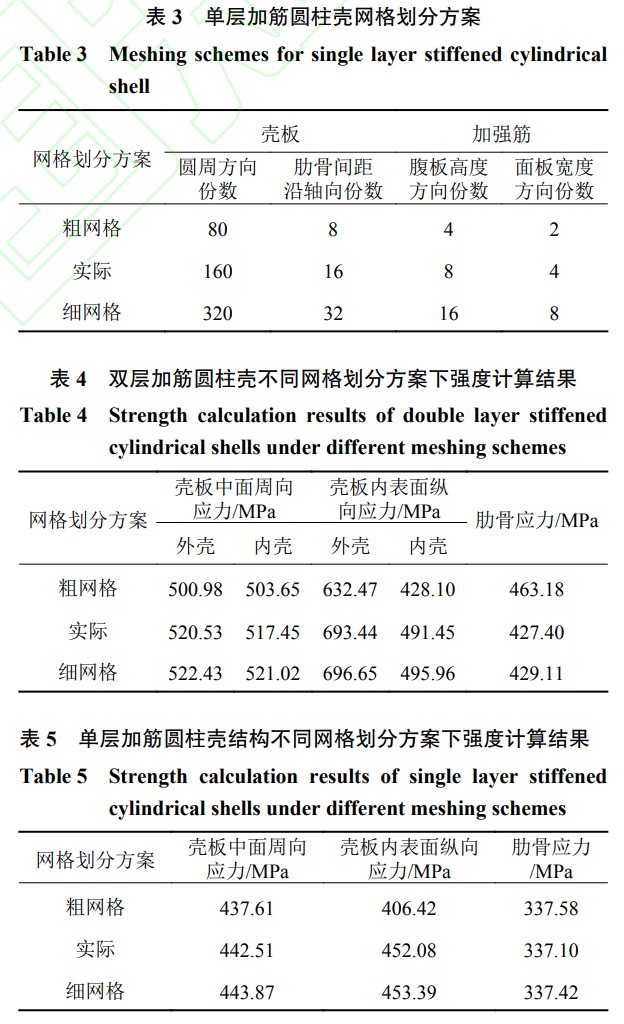
本文采用有限元軟件ANSYS對加筋圓柱殼結(jié)構(gòu)進行強度、穩(wěn)定性和極限承載能力計算。殼板與加強筋均采用Shell181單元進行模擬，采用映射網(wǎng)格予以劃分，在圓周方向劃分160等份，在肋骨腹板高度方向劃分8等份，在面板寬度方向劃分4等份，肋骨間距沿軸向劃分為16等份。針對長徑比L/D=1、計算壓力P=6MPa的雙層加筋圓柱殼結(jié)構(gòu)和L/D=2、計算壓力P=6MPa的單層加筋圓柱殼結(jié)構(gòu)的典型方案，在實際網(wǎng)格劃分方案的基礎上，分別采用粗網(wǎng)格劃分方案和細網(wǎng)格劃分方案進行強度計算，網(wǎng)格劃分方案如表2和表3所示，不同網(wǎng)格劃分方案下的強度計算結(jié)果如表4和表5所示。由表4可知，雙層加筋圓柱殼結(jié)構(gòu)粗網(wǎng)格方案下的強度計算結(jié)果與實際方案相比最大誤差為11.6%，細網(wǎng)格方案下的強度計算結(jié)果與實際方案相比誤差不超過1.0%。由表5可知，單層加筋圓柱殼結(jié)構(gòu)粗網(wǎng)格方案下的強度計算結(jié)果與實際方案相比最大誤差為10.1%，細網(wǎng)格方案下的強度計算結(jié)果與實際方案相比誤差不超過1.0%。這表明，計算采用的實際網(wǎng)格劃分方案滿足有限元分析收斂性要求。

1.4邊界條件與加載方式

鈦合金雙層加筋圓柱殼的軸線與z軸平行，坐標軸的x向為圓柱殼的徑向，y向為圓柱殼的周向。約束圓柱殼左端3個平動自由度ux=uy=uz=0，右端約束x（徑向）、y（周向）2個平動自由度ux=uy=0，軸向z平動自由度uz不約束。對于雙層加筋圓柱殼結(jié)構(gòu)，圓柱殼外殼受到大小為P的均布壓力，軸向載荷以縱向力的形式作用在內(nèi)、外殼板上。軸向載荷T與內(nèi)、外殼板單位寬度縱向力T₀，T₁之間的關系為：

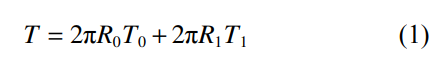
式中：T=πR₁²P；R1為雙層圓柱殼外殼半徑；R0為雙層圓柱殼內(nèi)殼半徑。根據(jù)結(jié)構(gòu)形式特點，可知內(nèi)、外殼板半徑差較小，且端部徑向轉(zhuǎn)動較小，因此可近似認為內(nèi)、外殼板軸向位移相同，通過材料力學理論，可得

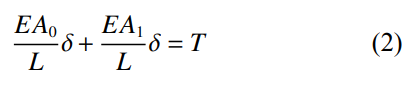
式中：L為內(nèi)、外殼板總長度；A0=2πR0t0，A1=2πR1t1，分別為內(nèi)、外殼板橫截面積，其中t0為雙層圓柱殼內(nèi)殼厚度，t1為雙層圓柱殼外殼厚度；δ為內(nèi)、外殼板的軸向位移。

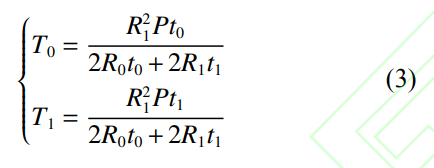
由式（1）和式（2），可得本文右端節(jié)點受到如下近似的等效軸向力。雙層圓柱殼外殼端部節(jié)點：

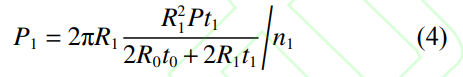
雙層圓柱殼內(nèi)殼端部節(jié)點：

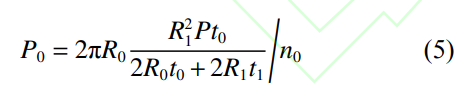
式中：n1為外殼端部周向節(jié)點數(shù)；n0為內(nèi)殼端部周向節(jié)點數(shù)。式（4）和式（5）計算結(jié)果與文獻[4]給出的計算式十分接近，相對誤差不到1%。對于單層加筋圓柱殼結(jié)構(gòu)，圓柱殼殼體受到大小為P的均布壓力，右端節(jié)點受到等效軸向節(jié)點力，大小如下：

式中：R為圓柱殼半徑；n為右端周向節(jié)點數(shù)。

2、優(yōu)化設計數(shù)學模型

2.1設計變量

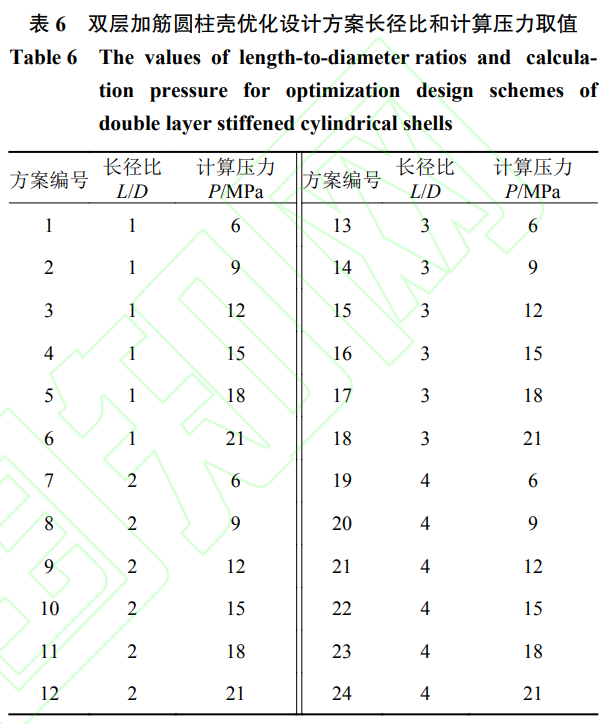
雙層加筋圓柱殼的長度L和半徑R1通常根據(jù)總體設計要求確定，本文選取圓柱殼內(nèi)殼厚度t0、外殼厚度t1、肋骨腹板高度h、腹板厚度t2、肋骨間距s這5個設計參數(shù)作為設計變量，直徑D保持不變，圓柱殼長度L和計算壓力P作為參變量。為了研究不同長徑比L/D和不同計算壓力P下優(yōu)化方案的差異，設置了24組不同長徑比和計算壓力取值的方案，不同優(yōu)化設計方案長徑比和計算壓力的取值如表6所示。

選取單層加筋圓柱殼殼板厚度T1、肋骨腹板高度H、肋骨腹板厚度T2、肋骨面板寬度W、肋骨面板厚度T3和肋骨間距S這6個設計參數(shù)作為設計變量，直徑D保持不變，圓柱殼長度L和計算壓力P作為參變量，為對比分析不同長徑比和不同計算壓力下單、雙層加筋圓柱殼優(yōu)化方案的差異，設置了6組典型的優(yōu)化設計方案，具體將在后面的3.4節(jié)予以介紹。

2.2約束條件

根據(jù)《水下結(jié)構(gòu)設計計算方法》，對于單、雙層加筋圓柱殼結(jié)構(gòu)，其計算深度h_c按下式計算：

式中：h_e為極限深度；K為安全系數(shù)，本文取1.5。在進行雙層加筋圓柱殼結(jié)構(gòu)優(yōu)化設計時，將內(nèi)殼中面周向應力、內(nèi)殼內(nèi)表面縱向應力、外殼中面周向應力、外殼內(nèi)表面縱向應力和肋骨應力這5個特征應力作為強度約束條件，其中內(nèi)殼中面周向應力和外殼中面周向應力約束如式（8）所示；內(nèi)殼內(nèi)表面縱向應力和外殼內(nèi)表面縱向應力約束如式（9）所示，肋骨應力約束如式（10）所示。

1）雙層加筋圓柱殼殼板（含內(nèi)、外殼板）的中面周向應力：

2）雙層加筋圓柱殼殼板（含內(nèi)、外殼板）內(nèi)表面縱向應力：

3）雙層加筋圓柱殼肋骨應力：

本文中，計算參數(shù)k₁，k₂，k₃分別取0.9，1.15和0.6。穩(wěn)定性包括殼板穩(wěn)定性和總體穩(wěn)定性。在有限元計算中，將第1階局部失穩(wěn)波形缺陷下的極限承載能力作為殼板穩(wěn)定性失穩(wěn)臨界壓力，第1階總體失穩(wěn)波形缺陷下的極限承載能力作為殼板總體穩(wěn)定性失穩(wěn)臨界壓力，其中，局部失穩(wěn)波形初始缺陷幅值取殼板厚度的0.2倍，總體失穩(wěn)波形初始缺陷幅值取圓柱殼半徑的0.25%。為節(jié)省計算時間，在優(yōu)化設計階段，通過控制結(jié)構(gòu)屈曲計算中第1階失穩(wěn)特征值的方式，近似地保證結(jié)構(gòu)的穩(wěn)定性要求。獲得優(yōu)化設計方案后，再通過有限元計算結(jié)構(gòu)方案的極限承載能力，確定結(jié)構(gòu)方案滿足局部穩(wěn)定性和總體穩(wěn)定性要求。第1階失穩(wěn)特征值要求如下：

式中：P_E1為第1階失穩(wěn)特征值；系數(shù)k₄取值0.4～0.6，具體取值視情確定。此外，雙層加筋圓柱殼腹板高度和厚度還需滿足如下關系：

在進行單層加筋圓柱殼結(jié)構(gòu)優(yōu)化設計時，將殼板中面周向應力、殼板內(nèi)表面縱向應力和肋骨應力這3個特征應力作為強度約束條件，滿足的要求如式（8）～式（10）所示，第1階失穩(wěn)特征值要求如式（11）所示。另外，單層加筋圓柱殼腹板高度和腹板的厚度需滿足如下關系：

單層加筋圓柱殼面板寬度和面板厚度需滿足如下關系：

單層加筋圓柱殼腹板和面板的厚度差需滿足如下關系：

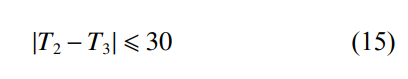
2.3目標函數(shù)

雙層加筋圓柱殼優(yōu)化設計的目標函數(shù)為其重量m，如下式所示：

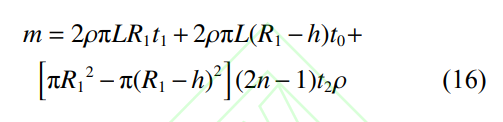
其中，當肋骨間距s能被L/2整除時，n=0.5L/s，否則，n=nint（0.5L/s?0.5）+1。單層加筋圓柱殼優(yōu)化設計的目標函數(shù)為其重量M，如下式所示：

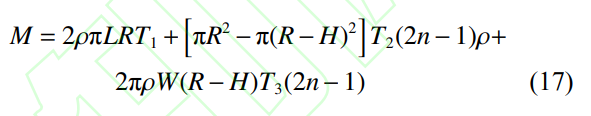
3、優(yōu)化設計結(jié)果與分析

3.1優(yōu)化設計方案分析

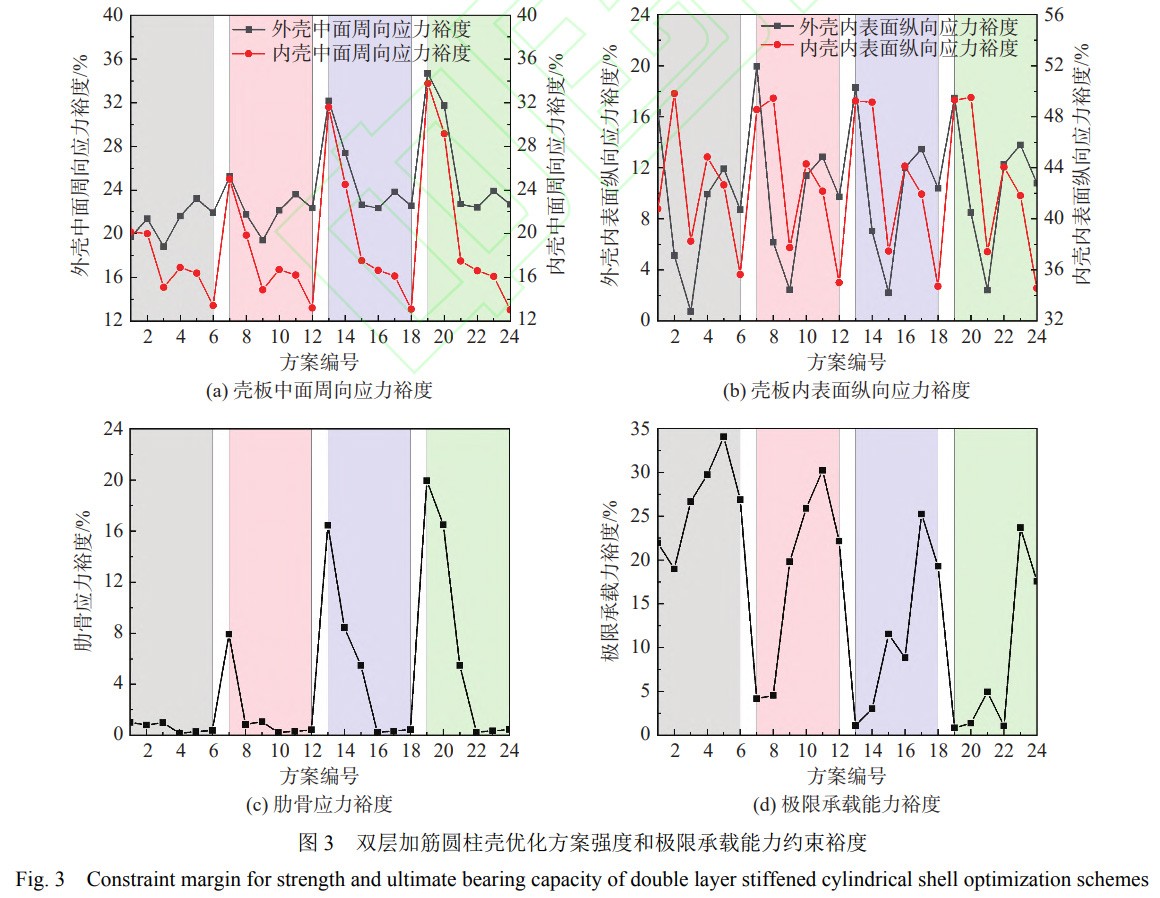
采用遺傳算法進行求解。初始群體個數(shù)取20，交叉概率取0.9，變異概率取0.01，最大迭代次數(shù)取100。取式（11）中系數(shù)k4的初始值為0.5，得到初步優(yōu)化方案后，采用有限元方法計算校核優(yōu)化方案的極限承載能力，對于不滿足極限承載能力約束的方案，降低系數(shù)k4的值，采用遺傳算法再次進行優(yōu)化求解，直至得到滿足極限承載能力要求的優(yōu)化方案；對于強度約束裕度或者極限承載能力約束裕度較大的方案，提高系數(shù)k4的值，采用遺傳算法再次進行優(yōu)化求解，直至得到強度約束裕度或者極限承載能力約束裕度接近邊界，并且滿足約束條件的優(yōu)化方案。雙層加筋圓柱殼不同優(yōu)化方案設計變量的取值如圖2所示，不同優(yōu)化方案強度和極限承載能力約束裕度如圖3所示。其中，極限承載能力為第1階局部失穩(wěn)波形初始缺陷下的極限承載能力和第1階總體失穩(wěn)波形初始缺陷下極限承載能力中的較小值，約束裕度=（限界值?計算值）/限界值×100%（小于等于型約束）或約束裕度=（計算值?限界值）/限界值×100%（大于等于型約束）。雙層加筋圓柱殼殼板中面周向應力和內(nèi)表面縱向應力主要受殼板厚度的影響，而肋骨應力主要受腹板尺寸的影響，因此在相同長徑比下，當計算壓力增大時，需要增大殼板厚度、腹板高度和厚度以滿足強度約束條件。

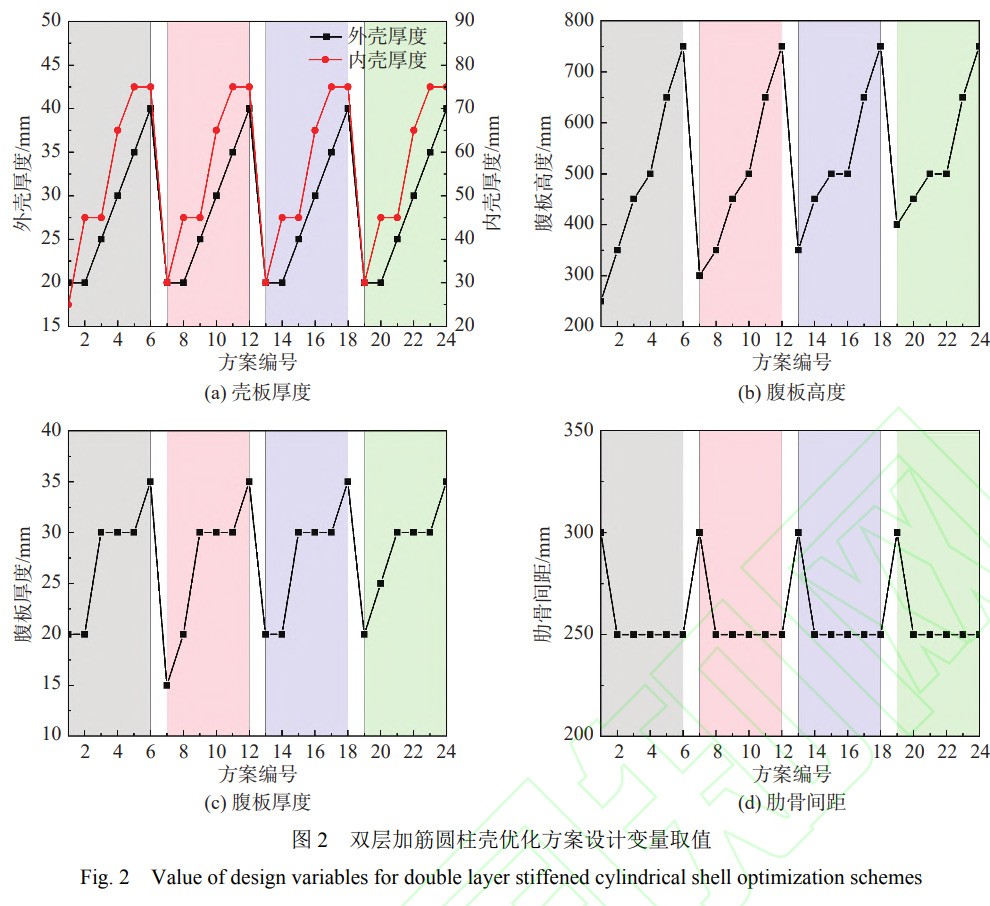
由圖2可看出，當計算壓力增大時，優(yōu)化方案的殼板厚度、腹板高度和腹板厚度基本呈線性增大的趨勢。此外還可以發(fā)現(xiàn)，在相同長徑比下，優(yōu)化方案的極限承載能力裕度也隨著計算壓力的增大呈增大的趨勢。由《水下結(jié)構(gòu)設計計算方法》可知，作為強度約束的特征應力為PR/t的函數(shù)，而殼板穩(wěn)定性失穩(wěn)臨界壓力即局部失穩(wěn)特征值為(t/R)²（其中t為加筋圓柱殼殼板厚度）的函數(shù)，總體穩(wěn)定性失穩(wěn)臨界壓力即總體失穩(wěn)特征值為(t³+Ah²)/R³（其中A為肋骨橫剖面積）的函數(shù)。這就導致當計算壓力增大時，優(yōu)化方案殼板厚度近似呈線性增加，而局部失穩(wěn)臨界壓力近似呈殼板厚度的平方增加，總體失穩(wěn)臨界壓力近似呈殼板厚度的三次方增加，因此極限承載能力增大的幅度遠大于計算壓力增大的幅度，即計算壓力越大，優(yōu)化方案的極限承載裕度越大。在一些特定的計算壓力下，不同長徑比優(yōu)化方案的設計變量取值完全相同，且特征應力大小基本相等，而極限承載能力則隨長徑比的增大而減小。由《水下結(jié)構(gòu)設計計算方法》中的分析可得，當不同優(yōu)化方案的設計變量取值完全相同時，PR/t相等，因此特征應力計算值完全相等，表現(xiàn)為特征應力有限元計算值基本相等，而總體穩(wěn)定性失穩(wěn)臨界壓力計算系數(shù)隨著長度L的增大而減小，所以總體穩(wěn)定性失穩(wěn)臨界壓力也隨長度L的增大而減小，即總體失穩(wěn)極限承載能力隨長徑比的增大而減小。由圖3可知，優(yōu)化方案的外殼中面周向應力、內(nèi)殼中面周向應力和內(nèi)殼內(nèi)表面縱向應力的約束裕度較為富裕，接近邊界的約束為外殼內(nèi)表面縱向應力、肋骨應力和極限承載能力，也即強度積極約束為外殼內(nèi)表面縱向應力約束和肋骨約束。因此，可以將所有優(yōu)化方案分為3種類型：穩(wěn)定性約束型、強度約束型以及強度和穩(wěn)定性共同約束型。穩(wěn)定性約束型指優(yōu)化方案僅有極限承載能力接近約束限界，其他約束裕度較大，也即此方案的積極約束為極限承載能力約束；強度約束型是指優(yōu)化方案僅有外殼內(nèi)表面縱向應力和肋骨應力兩者之一或者兩者均接近約束限界，其他約束裕度較大，也即此方案的積極約束為強度積極約束；強度和穩(wěn)定性共同約束型是指優(yōu)化方案的極限承載能力、外殼內(nèi)表面縱向應力和肋骨應力的兩者或其中之一接近約束限界，其他約束裕度較大，也即此方案的積極約束為強度和極限承載能力約束。

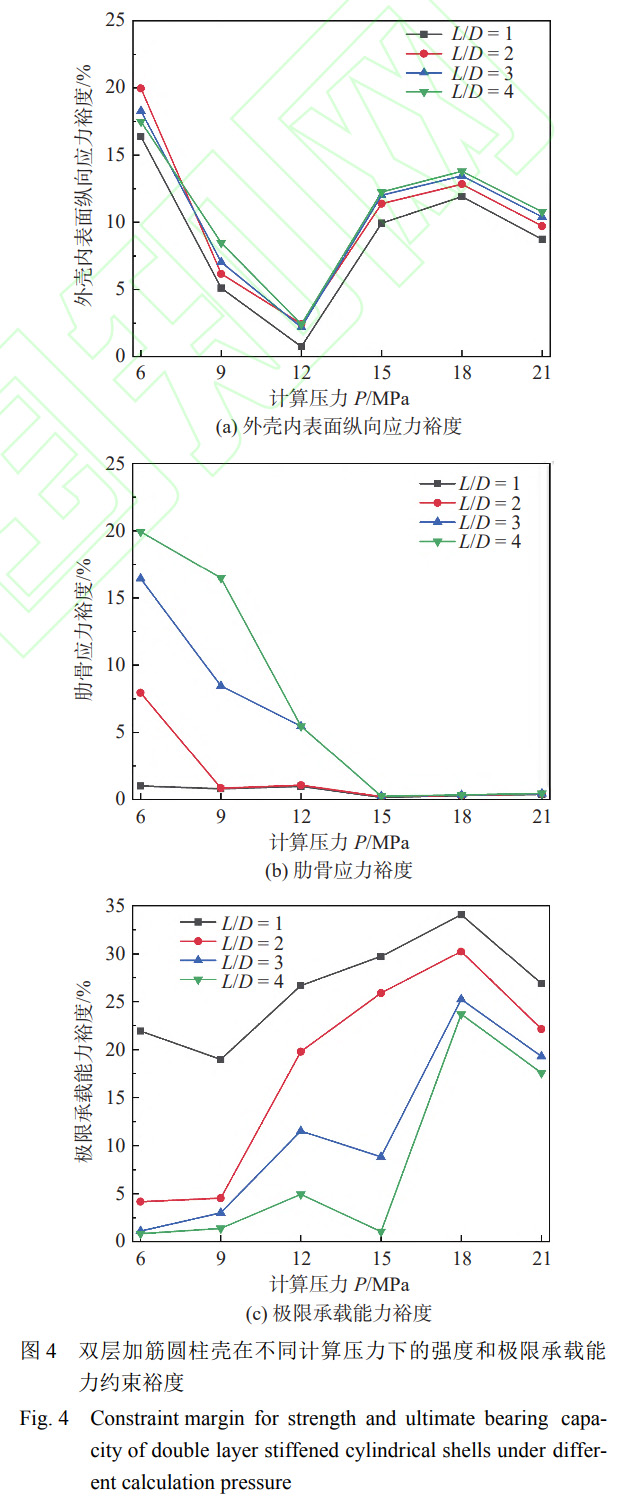
3.2不同計算壓力對優(yōu)化設計的影響及分析

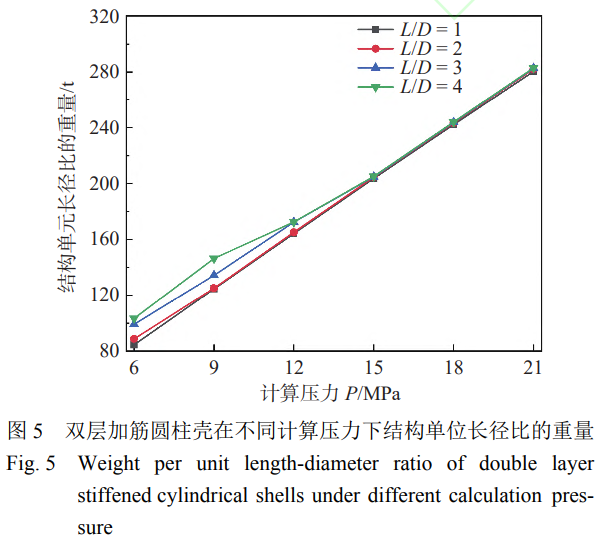
不同計算壓力下優(yōu)化方案的強度約束裕度（外殼內(nèi)表面縱向應力、肋骨應力）和極限承載能力約束裕度如圖4所示。當長徑比L/D=1時，6個不同計算壓力的優(yōu)化方案的強度約束接近約束限界，而極限承載能力約束裕度較大，即6個優(yōu)化方案的優(yōu)化類型均為強度約束型。當長徑比L/D=2、計算壓力P=6MPa時，優(yōu)化方案的強度約束裕度較大，極限承載能力接近約束限界，也即此方案的優(yōu)化類型為穩(wěn)定性約束型；而當計算壓力增大至9MPa時，強度約束和極限承載能力約束均接近于約束限界，也即此方案的優(yōu)化類型為共同約束型；當計算壓力再次增大時，極限承載能力裕度增大的幅度遠大于計算壓力增大的幅度，剩下4個方案的極限承載能力約束裕度均較大，優(yōu)化類型均為強度約束型。長徑比L/D=3，4的優(yōu)化方案也存在類似的規(guī)律，即隨著計算壓力額增大，優(yōu)化方案類型會發(fā)生變化。對于長徑比一定的鈦合金雙層加筋圓柱殼優(yōu)化設計，基本分為3個類型：第1個類型是當計算壓力小于某個臨界值（記為Pc1）時，滿足極限承載能力要求的設計變量的取值大于滿足強度約束要求的設計變量取值，因此，極限承載能力約束接近于約束限界，而強度約束裕度比較大，主要是極限承載能力約束控制優(yōu)化設計，優(yōu)化類型為穩(wěn)定性約束型；第2個類型是當計算壓力大于Pc1而小于另一個臨界值（記為Pc2）時，強度約束和極限承載能力約束均接近于約束限界，主要是強度約束和極限承載能力約束同時控制優(yōu)化設計，優(yōu)化類型為共同約束型；第3個類型是當計算壓力大于Pc2時，隨著計算壓力的增大，極限承載能力增大的幅度遠大于計算壓力增大的幅度，因此當強度約束接近于約束限界時，極限承載能力裕度比較大，主要是強度約束控制優(yōu)化設計，優(yōu)化類型為強度約束型。對于長徑比為1的雙層加筋圓柱殼結(jié)構(gòu)，臨界計算壓力值Pc1和Pc2均小于6MPa。為了更直觀地體現(xiàn)不同優(yōu)化方案之間的重量差異，將結(jié)構(gòu)重量歸一化，給出不同計算壓力下優(yōu)化方案單位長徑比的重量（即結(jié)構(gòu)重量/長徑比）如圖5所示。當長徑比一定時，隨著計算壓力的增大，優(yōu)化方案設計變量的取值增大，重量也逐漸增大；當計算壓力P<15MPa時，隨著長徑比的增大，單位長徑比的重量基本呈線性增大的趨勢；當計算壓力P>15MPa時，由于不同長徑比優(yōu)化方案設計變量的取值相同，因此單位長徑比的重量也基本相等。

3.3不同長徑比對優(yōu)化設計的影響及分析

不同長徑比下優(yōu)化方案的強度約束裕度（外殼內(nèi)表面縱向應力、肋骨應力）和極限承載能力約束裕度如圖6所示。

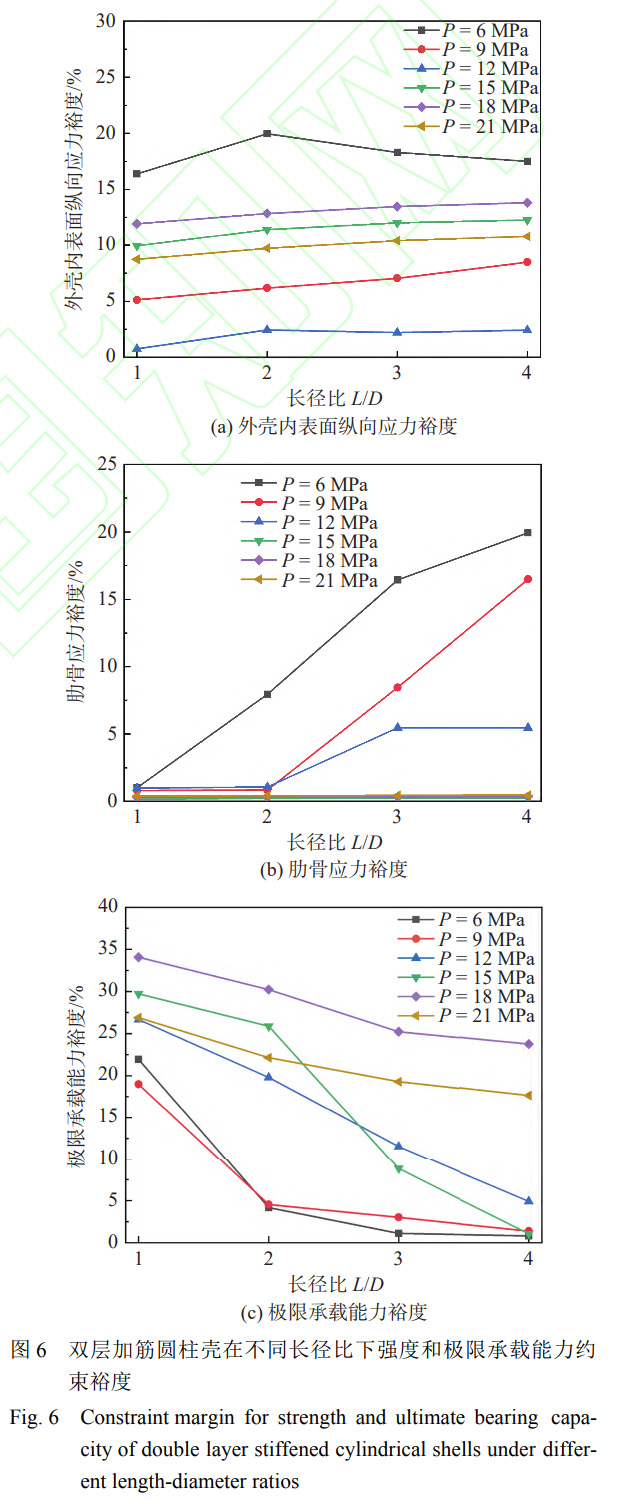
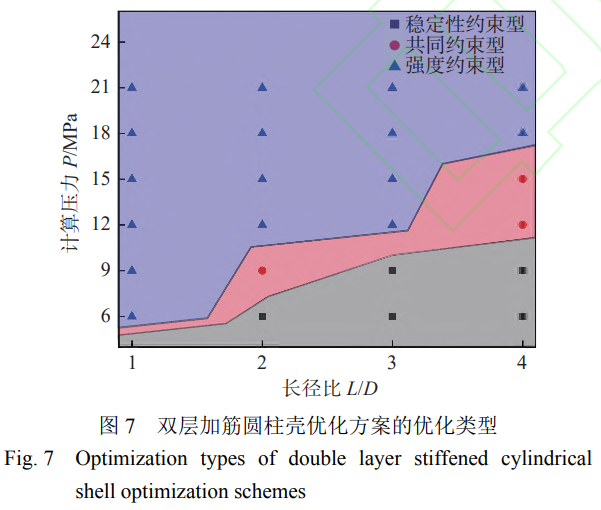
當計算壓力一定、長徑比增大時，為了滿足極限承載能力約束要求，優(yōu)化方案的設計變量取值可能需要進一步增大，這就導致優(yōu)化類型有可能發(fā)生改變。計算壓力P=9MPa、長徑比L/D=2時，優(yōu)化方案類型為共同約束型，當長徑比L/D增大為3時，此時原設計變量取值已不能滿足極限承載能力要求，腹板高度由350mm增大為450mm，強度約束裕度增大，優(yōu)化方案類型為穩(wěn)定性約束型。當計算壓力P=12MPa、長徑比L/D=3時，優(yōu)化方案類型為強度約束型，當長徑比L/D增大為4時，雖然優(yōu)化方案設計變量的取值未改變，但是由于極限承載能力降低，優(yōu)化方案類型變?yōu)楣餐s束型。其他計算壓力下的優(yōu)化方案也存在類似的規(guī)律，即隨著長徑比的增大，優(yōu)化方案類型會發(fā)生變化。對于鈦合金雙層加筋圓柱殼優(yōu)化設計，長徑比越大，第1種類型（優(yōu)化類型為穩(wěn)定性約束型）的臨界計算壓力值Pc1越大，第2種類型（優(yōu)化類型為共同約束型）的臨界計算壓力值Pc2也越大。給出24個優(yōu)化方案的優(yōu)化設計類型散點圖如圖7所示。3種散點的形狀代表3種優(yōu)化設計類型，圖中的2條曲線為根據(jù)優(yōu)化方案類型變化擬合得到的臨界計算壓力值Pc1和Pc2的曲線，圖中有3個不同的顏色區(qū)域，從下至上分別代表優(yōu)化類型為穩(wěn)定性約束型、共同約束型和強度約束型區(qū)域。在進行鈦合金雙層加筋圓柱殼優(yōu)化設計時，可以通過該圖估計某一長徑比與計算壓力的搭配時優(yōu)化設計的類型，也可以估計不同長徑比時的臨界計算壓力值Pc1和Pc2。在進行優(yōu)化設計時，可以先判斷優(yōu)化類型，以此改變優(yōu)化設計數(shù)學模型中相應的約束，例如取消某個約束，從而更快速、高效地得到優(yōu)化方案。例如當優(yōu)化類型為強度約束型時，可以不考慮第1階失穩(wěn)特征值這一約束條件，從而快速得到重量最輕的優(yōu)化方案。

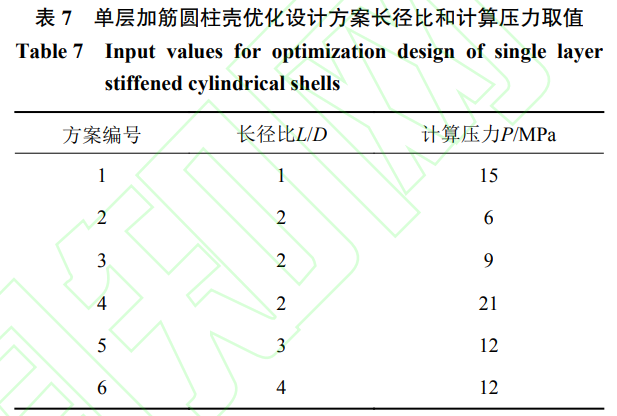
3.4與單層加筋圓柱殼優(yōu)化方案的對比分析

為了對比雙層加筋圓柱殼與單層加筋圓柱殼優(yōu)化方案間的差異，選擇了包括4個長徑比、3種設計類型的共計6組優(yōu)化設計方案。單層加筋圓柱殼不同方案下的長徑比和計算壓力取值如表7所示，相同設計輸入下單、雙層加筋圓柱殼優(yōu)化方案的重量如圖8所示，強度、極限承載能力約束裕度的對比如圖9所示。從中可以發(fā)現(xiàn)，雙層加筋圓柱殼的重量始終低于單層加筋圓柱殼，約低4.0%～16.8%，且雙層加筋圓柱殼的極限承載能力高于單層加筋圓柱殼。單層加筋圓柱殼的強度積極約束為肋骨應力約束，且在相同設計輸入下，單層加筋圓柱殼優(yōu)化方案的優(yōu)化類型可能發(fā)生變化。例如，當計算壓力P=9MPa、長徑比L/D=2時，雙層加筋圓柱殼優(yōu)化方案的外殼內(nèi)表面縱向應力、肋骨應力和極限承載能力約束均接近邊界，優(yōu)化類型為共同約束型，而單層加筋圓柱殼優(yōu)化方案僅極限承載能力約束接近邊界，優(yōu)化方案為穩(wěn)定性約束型。

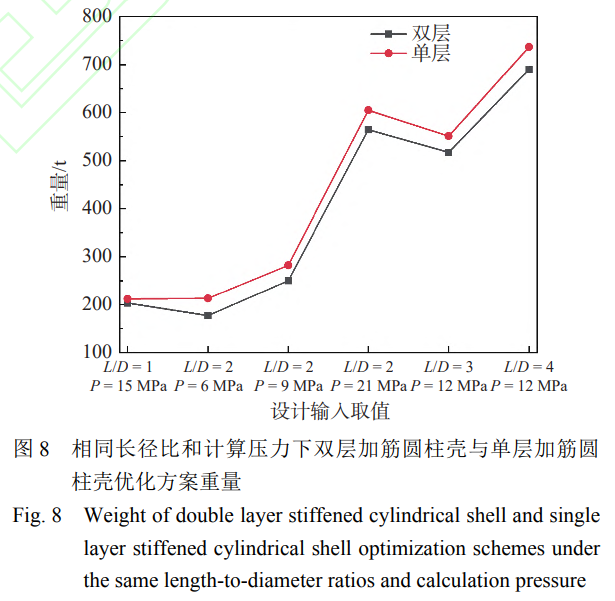
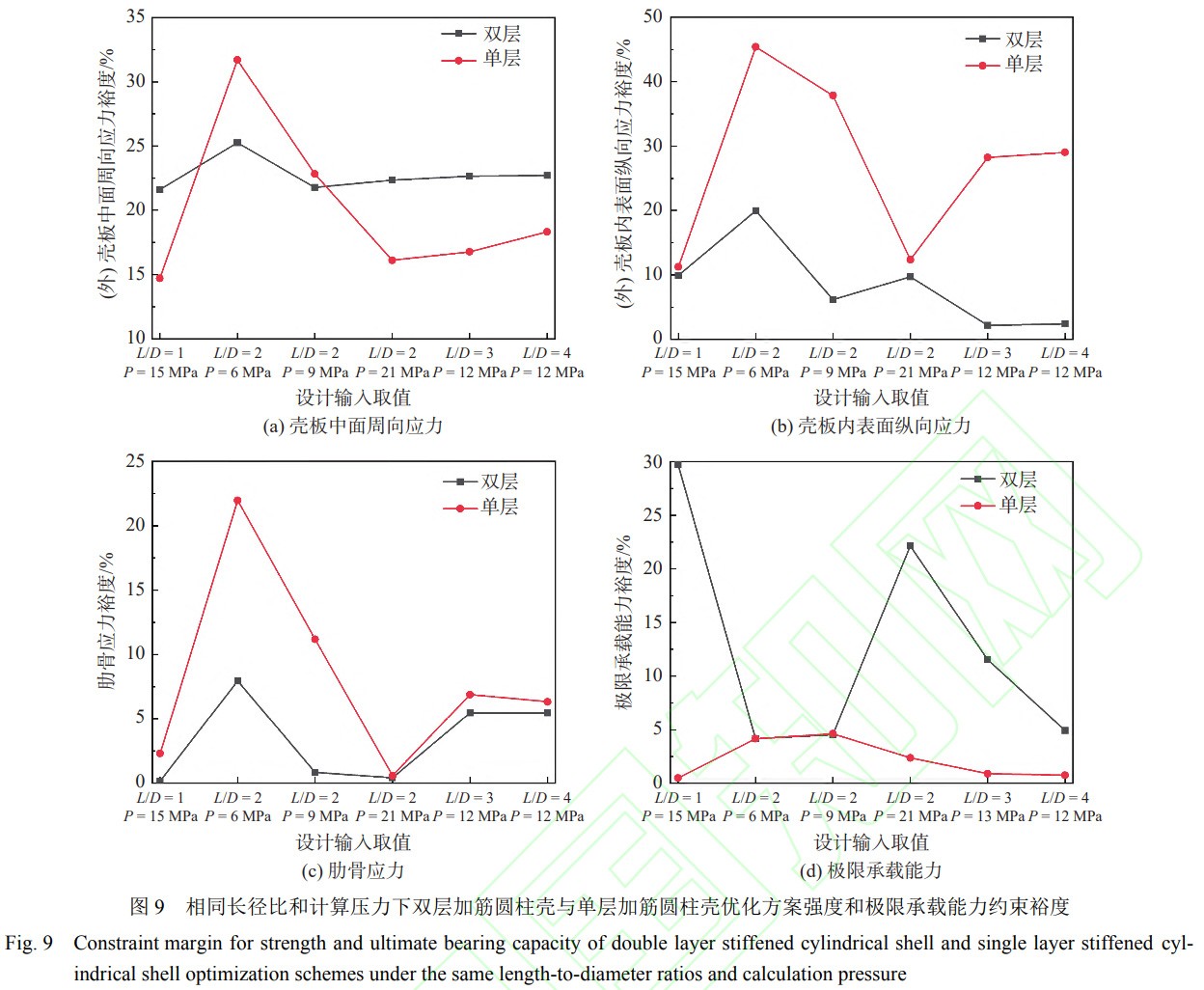
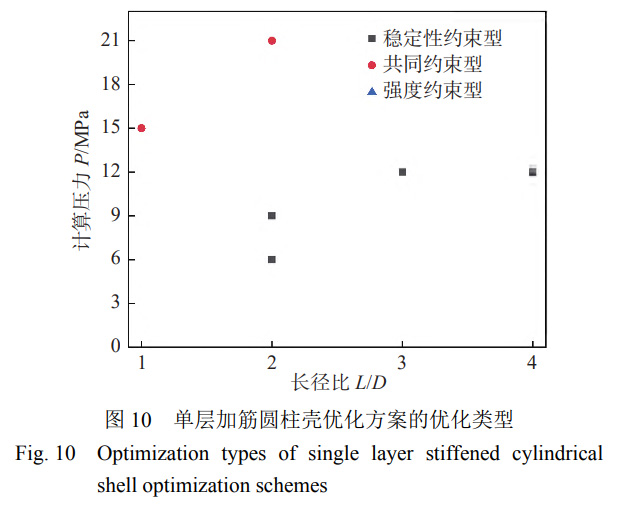
單層加筋圓柱殼優(yōu)化方案的優(yōu)化類型散點圖如圖10所示。經(jīng)與雙層加筋圓柱殼優(yōu)化方案的優(yōu)化類型散點圖對比可以發(fā)現(xiàn)，在相同長徑比下，鈦合金雙層加筋圓柱殼優(yōu)化設計的臨界計算壓力值Pc1和Pc2相比單層加筋圓柱殼優(yōu)化設計的臨界計算壓力值更小。這是因為在相同設計輸入下，雙層加筋圓柱殼優(yōu)化方案的極限承載能力高于單層加筋圓柱殼，當優(yōu)化類型為強度約束型時，由強度約束控制優(yōu)化設計，極限承載能力裕度較大，當計算壓力降低時，雙層加筋圓柱殼極限承載能力降低的幅度比單層加筋圓柱殼的更緩慢。因此，雙層加筋圓柱殼的臨界計算壓力值Pc2比單層加筋圓柱殼的小，同理可知，雙層加筋圓柱殼的臨界計算壓力值Pc1也比單層加筋圓柱殼的小。

4、結(jié)論

本文以雙層加筋圓柱殼結(jié)構(gòu)為研究對象，重點探究了不同長徑比和不同計算壓力下鈦合金雙層加筋圓柱殼優(yōu)化設計方案的設計變量、重量、特征應力裕度以及極限承載能力裕度之間的差異，主要得到如下結(jié)論：

1）對于某一長徑比的鈦合金雙層加筋圓柱殼優(yōu)化設計，存在2個臨界計算壓力值Pc1和Pc2，當計算壓力值小于Pc1時，主要是極限承載能力約束控制優(yōu)化設計，優(yōu)化類型為穩(wěn)定性約束型；當計算壓力值大于Pc1而小于Pc2時，主要是強度約束和極限承載能力約束同時控制優(yōu)化設計，優(yōu)化類型為共同約束型；當計算壓力值大于Pc2時，主要是強度約束控制優(yōu)化設計，優(yōu)化類型為強度約束型。

2）對于鈦合金雙層加筋圓柱殼優(yōu)化設計，長徑比越大，臨界計算壓力值Pc1越大，臨界計算壓力值Pc2也越大。長徑比L/D=1的鈦合金雙層加筋圓柱殼的臨界計算壓力值Pc1和Pc2均小于6MPa；長徑比L/D=2的鈦合金雙層加筋圓柱殼的臨界計算壓力值Pc1在6～9MPa范圍內(nèi)，Pc2在9～12MPa范圍內(nèi)；長徑比L/D=3的鈦合金雙層加筋圓柱殼的臨界計算壓力值Pc1和Pc2均在9～12MPa范圍內(nèi)；長徑比L/D=4的鈦合金雙層加筋圓柱殼的臨界計算壓力值Pc1在9～12MPa范圍內(nèi)，Pc2在15～18MPa范圍內(nèi)。

3）對于鈦合金加筋圓柱殼結(jié)構(gòu)優(yōu)化設計，在相同的計算壓力和長徑比下，雙層加筋圓柱殼優(yōu)化方案的重量始終低于單層加筋圓柱殼，約低4.0%～16.8%；在相同長徑比下，雙層加筋圓柱殼優(yōu)化設計的臨界計算壓力值Pc1和Pc2相比單層加筋圓柱殼優(yōu)化設計的臨界計算壓力值要小。

參考文獻：

[1]唐其琴, 李伯陽, 丁志偉, 等. 軸壓載荷下夾層圓柱殼結(jié) 構(gòu) 屈 曲 承 載 力 優(yōu) 化 [J]. 機 械 設 計與 制 造 , 2020(8): 80–84.

TANG Q Q, LI B Y, DING Z W, et al. Optimization of buckling capability of sandwich cylindrical shell structures under axial compression load[J]. Machinery Design & Manufacture, 2020(8): 80–84 (in Chinese).

[2]胡子嘯, 李世強, 劉子晗, 等. 雙層耐壓加筋圓柱殼結(jié)構(gòu) 承載能力與抗爆性能分析 [J]. 中國艦船研究, 2024, 19(3): 205–216.

HU Z X, LI S Q, LIU Z H, et al. Analysis on the bearing capacity and blast resistance of pressure stiffened double cylindrical shell structure[J]. Chinese Journal of Ship Research,2024, 19(3): 205–216 (in Chinese).

[3]夏賢坤, 謝祚水. 夾層圓柱殼結(jié)構(gòu)的應力與總穩(wěn)定性分 析 [J]. 華東船舶工業(yè)學院學報 (自然科學版),2004, 18(1): 10–12.

XIA X K, XIE Z S. Stress and stability analysis of double shell structure[J]. Journal of East China Shipbuilding Institute (Natural Science Edition), 2004, 18(1): 10–12 (in Chinese).

[4]曹曉明, 喻衛(wèi)寧, 王磊, 等. 環(huán)向加筋夾層圓柱殼體應力 計 算 方 法 [J]. 哈 爾 濱 工 程 大 學 學報 , 2023, 44(2): 181–189.

CAO X M, YU W N, WANG L, et al. Stress analysis of ring-stiffened sandwich cylindrical shells [J]. Journal of Harbin Engineering University, 2023, 44(2): 181–189 (in Chinese)

[5]夏賢坤, 謝祚水. 夾層圓柱殼結(jié)構(gòu)的優(yōu)化設計 [J]. 中國 造船, 2006, 47(3): 130–133. XIA X K,XIE Z S. Optimization design of cylindrical interlayer shell structure[J]. Shipbuilding of China, 2006, 47(3): 130–133 (in Chinese).

[6]DING H X. Strength and stability of double cylindrical shell structure subjected to hydrostatic external pressure —II: stability[J]. Marine structures, 2003, 16(5): 397–415.

[7] XUE J H, WANG Y O, YUAN D. A shear deformation theory for bending and buckling of undersea sandwich pipes[J]. Composite Structures, 2015, 132: 633–643.

[8]江翔. 鈦合金圓柱耐壓殼沖擊作用下的承載能力分析[D]. 鎮(zhèn)江: 江蘇科技大學, 2020.

JIANG X. Analysis of bearing capacity of cylindrical pressure shell under impact[D].Zhenjiang: Jiangsu University of Science and Technology, 2020 (in Chinese).

[9]李艷萍. 大深度水下耐壓殼體的結(jié)構(gòu)初步設計與優(yōu)化[D]. 上海: 上海交通大學, 2020.

LI Y P. Preliminary design and optimization of the structure of a hull under ultra depth water[D]. Shanghai: Shanghai Jiao Tong University, 2020 (in Chinese).

[10]GE K K, YU Y, XU Q, et al. Analysis of residual stresses and distortions of a titanium alloy ring-stiffened cylindrical shell[J]. Materials Testing, 2022, 64(1): 98–104.

[11]劉楨. 考慮碰撞凹陷的鈦合金耐壓殼屈曲研究 [D]. 鎮(zhèn) 江: 江蘇科技大學, 2020.

LIU Z. Research on buckling of titanium alloy pressure shell considering impact depression[D].Zhenjiang: Jiangsu University of Science and Technology, 2020 (in Chinese).

[12]ZHANG B W, YU X Y, WAN Z Q, et al. Research on the failure characteristics analysis of the titanium alloy ring-stiffened cylindrical shell based on damage evolution[C]//Proceedings of the 12th International Conference on Quality, Reliability, Risk, Maintenance, and Safety Engineering (QR2MSE 2022). Emeishan, China: IEEE, 2022: 2126?2131.

[13]曹曉明, 李釗, 王磊, 等. 基于粒子群算法的環(huán)向加筋夾 層圓柱殼體優(yōu)化設計 [J]. 艦船科學技術(shù),2023, 45(2): 23–28.

CAO X M, LI Z, WANG L, et al. Design of ringstiffened sandwich cylindrical shells based on particle swarm optimization[J]. Ship Science and Technology, 2023, 45(2): 23–28 (in Chinese).

[14]汪靜, 王偉奇, 朱曉培, 等. 海底觀測儀耐壓殼體強度特 性研究 [J]. 機械科學與技術(shù), 2021, 40(3): 377–381.

WANG J, WANG W Q, ZHU X P, et al. Research on strength characteristics of seabed observer pressure hull[J]. Mechanical Science and Technology for Aerospace Engineering, 2021, 40(3):377–381 (in Chinese).

[15]張浩宇, 賀章勛, 程遠勝. 鈦合金耐壓夾層圓柱殼芯層 結(jié) 構(gòu) 拓 撲 優(yōu) 化 [J]. 中 國 艦 船 研 究, 2023, 18(2): 121–126,159.

ZHANG H Y, HE Z X, CHENG Y S. Topology optimization of core structure of titanium alloy sandwich cylindrical shell[J]. Chinese Journal of Ship Research, 2023, 18(2): 121–126,159 (inChinese).

相關鏈接